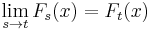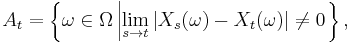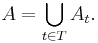Continuous stochastic process
In the probability theory, a continuous stochastic process is a type of stochastic process that may be said to be "continuous" as a function of its "time" or index parameter. Continuity is a nice property for (the sample paths of) a process to have, since it implies that they are well-behaved in some sense, and, therefore, much easier to analyse. It is implicit here that the index of the stochastic process is a continuous variable. Note that some authors[1] define a "continuous (stochastic) process" as only requiring that the index variable be continuous, without continuity of sample paths: in some terminology, this would be a continuous-time stochastic process, in parallel to a "discrete-time process". Given the possible confusion, caution is needed.[1]
Contents |
Definitions
Let (Ω, Σ, P) be a probability space, let T be some interval of time, and let X : T × Ω → S be a stochastic process. For simplicity, the rest of this article will take the state space S to be the real line R, but the definitions go through mutatis mutandis if S is Rn, a normed vector space, or even a general metric space.
Continuity with probability one
Given a time t ∈ T, X is said to be continuous with probability one at t if
Mean-square continuity
Given a time t ∈ T, X is said to be continuous in mean-square at t if E[|Xt|2] < +∞ and
Continuity in probability
Given a time t ∈ T, X is said to be continuous in probability at t if, for all ε > 0,
Equivalently, X is continuous in probability at time t if
Continuity in distribution
Given a time t ∈ T, X is said to be continuous in distribution at t if
for all points x at which Ft is continuous, where Ft denotes the cumulative distribution function of the random variable Xt.
Sample continuity
X is said to be sample continuous if Xt(ω) is continuous in t for P-almost all ω ∈ Ω. Sample continuity is the appropriate notion of continuity for processes such as Itō diffusions.
Feller continuity
X is said to be a Feller-continuous process if, for any fixed t ∈ T and any bounded, continuous and Σ-measurable function g : S → R, Ex[g(Xt)] depends continuously upon x. Here x denotes the initial state of the process X, and Ex denotes expectation conditional upon the event that X starts at x.
Relationships
The relationships between the various types of continuity of stochastic processes are akin to the relationships between the various types of convergence of random variables. In particular:
- continuity with probability one implies continuity in probability;
- continuity in mean-square implies continuity in probability;
- continuity with probability one neither implies, nor is implied by, continuity in mean-square;
- continuity in probability implies, but is not implied by, continuity in distribution.
It is tempting to confuse continuity with probability one with sample continuity. Continuity with probability one at time t means that P(At) = 0, where the event At is given by
and it is perfectly feasible to check whether or not this holds for each t ∈ T. Sample continuity, on the other hand, requires that P(A) = 0, where
Note that A is an uncountable union of events, so it may not actually be an event itself, so P(A) may be undefined! Even worse, even if A is an event, P(A) can be strictly positive even if P(At) = 0 for every t ∈ T. This is the case, for example, with the telegraph process.
Notes
References
- Kloeden, Peter E.; Platen, Eckhard (1992). Numerical solution of stochastic differential equations. Applications of Mathematics (New York) 23. Berlin: Springer-Verlag. pp. 38–39;. ISBN 3-540-54062-8.
- Øksendal, Bernt K. (2003). Stochastic Differential Equations: An Introduction with Applications (Sixth edition ed.). Berlin: Springer. ISBN 3-540-04758-1. (See Lemma 8.1.4)
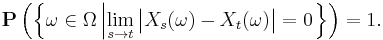
![\lim_{s \to t} \mathbf{E} \left[ \big| X_{s} - X_{t} \big|^{2} \right] = 0.](/2012-wikipedia_en_all_nopic_01_2012/I/94f0ca87b1efe8fbae48b9b7159b83a1.png)
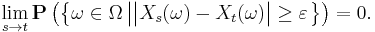
![\lim_{s \to t} \mathbf{E} \left[ \frac{\big| X_{s} - X_{t} \big|}{1 %2B \big| X_{s} - X_{t} \big|} \right] = 0.](/2012-wikipedia_en_all_nopic_01_2012/I/aa83e869e1daa28daa4ed027635d0159.png)